Volume of a Combination of Solids

A right circular cone of height $30 \mathrm{cm}$ is cut and removed by a plane parallel to its base from the vertex. If the volume of smaller cone obtained is $\frac{1}{27}$ of the volume of the given cone. Calculate the height of the remaining part of the cone.

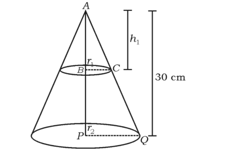
The base radius and height of a right circular cylinder and a right circular cone are equal and, if the volume of the cylinder is $360 {\mathrm{cm}}^3$, then the volume of a cone is

A solid is in the form of a cone mounted on a right circular cylinder, both having same radii as shown in the figure. The radius of the base and height of the cone are $7 \mathrm{cm}$ and $9 \mathrm{cm}$ respectively. If the total height of the solid is $30 \mathrm{cm}$, find the volume of the solid.

A hemispherical vessel of radius $14 cm$ is fully filled with sand. This sand is poured on level ground. The heap of sand forms a cone shape of height $7 cm$. If the area of ground occupied by the circular base of the heap of the sand is $k c{m}^2$, then find the value of $k$.

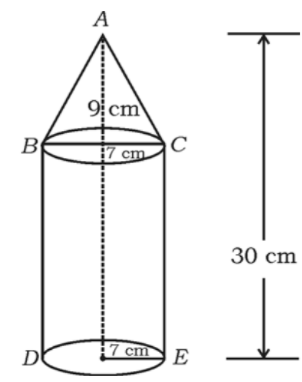
The bottom of a right cylindrical-shaped vessel made from the metallic sheet is closed by a cone-shaped vessel as shown in the figure. The radius of the circular base of the cylinder and radius of the circular base of the cone are each is equal to $7 cm$. If the height of the cylinder is $20 cm$ and the height of the cone is $3 cm$, If the cost of milk to fill completely this vessel at the rate of Rs. $20$ per litre is $₹ k$, then find the value of $k$.

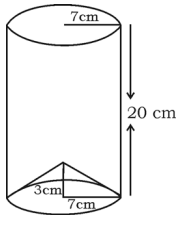
The radii of two circular ends of a frustum of a cone-shaped dustbin are $15 cm \& 8 cm.$ If its depth is $63 cm$ and the volume of the dustbin is $k c{m}^3$, then find the value of $k$.